词语解释:
zhěng chú
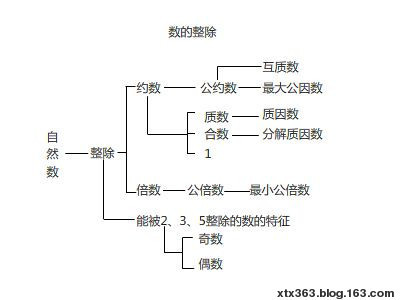
对于两个整数a、b(b≠0),若有一个整数q,使得a=bq,就称b整除a,或a被b整除,记作b|a。上述q即a除以b的商。类似地,x的两个多项式相除,如果得到的商仍是x的多项式,也称为整除。
用整除造句

词语解释:
zhěng chú
对于两个整数a、b(b≠0),若有一个整数q,使得a=bq,就称b整除a,或a被b整除,记作b|a。上述q即a除以b的商。类似地,x的两个多项式相除,如果得到的商仍是x的多项式,也称为整除。
整除造句:共找到27条整除的句子、用整除造句大全、用整除写一句话、用整除造句子,你还可以找到大量整除的优美例句、素材以及在文章中的用法等信息。